Redemption Yield
The redemption yield, also known as the yield to maturity (YTM) or gross redemption yield is the most frequently used measure of return from holding a bond. Yield to maturity takes into account the pattern of coupon payments, the bondís term to maturity and the capital gain (or loss) arising over the remaining life of the bond. The redemption yield is actually the similar measurement to the internal rate of return (IRR) of a series of cashflows, applied to a bond which is also a series of cashflows. If we set the IRR for a set of cash flows to be the rate that applies from a start-date to an end-date we can assume the IRR to be the YTM for those cash flows. The YTM therefore is equivalent to the internal rate of return on the bond, the rate that equates the value of the discounted cash flows on the bond to its current price. The calculation assumes that the bond is held until maturity and therefore it is the cash flows to maturity that are discounted in the calculation. It also employs the concept of the time value of money.
The formula for YTM is essentially that for calculating the price of a bond. For a bond paying annual coupons the YTM is calculated by solving equation (1), and we assume that the first coupon will be paid exactly one interest period now (which, for an annual coupon bond is exactly one year from now).
![]() †††††† (1)
†††††† (1)
where
Pd††††††† is the bond dirty price
C†††††††† is the coupon rate
M†††††††† is the par or redemption payment (100)
rm††††††† is the annual yield to maturity (the YTM)
n††††††††† the number of interest periods
Note that the number of interest periods in an annual-coupon bond are equal to the number of years to maturity, and so for these bonds n is equal to the number of years to maturity.
We can simplify (1) using
![]() where
where
![]() means ďis the sum ofĒ.
means ďis the sum ofĒ.
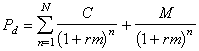 ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (2)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (2)
Note that the expression at 4.5 has two variable parameters, the price Pd and yield rm. It cannot be re-arranged to solve for yield rm explicitly and in fact the only way to solve for the yield is to use the process of numerical iteration. The process involves estimating a value for rm and calculating the price associated with the estimated yield. If the calculated price is higher than the price of the bond at the time, the yield estimate is lower than the actual yield, and so it must be adjusted until it converges to the level that corresponds with the bond price.
For YTM for a semi-annual coupon bond we have to adjust the formula to allow for the semi-annual payments. Equation (2) is modified as shown by (3) again assuming there are precisely six months to the next coupon payment.
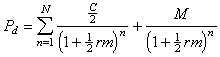 †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (3)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (3)
where n is the now the number of interest periods in the life of the bond and therefore equal to the number of years to maturity multiplied by 2.
All the YTM equations above use rm to discount a bondís cash flows back to the next coupon payment and then discount the value at that date back to the date of the calculation. In other words rm is the internal rate of return (IRR) that equates the value of the discounted cash flows on the bond to the current dirty price of the bond (at the current date). The internal rate of return is the discount rate which, if applied to all of the cash flows will solves for a number that is equal to the dirty price of the bond (its present value). By assuming that this rate will be unchanged for the reinvestment of all the coupon cash flows, and that the instrument will be held to maturity, the IRR can then be seen as the yield to maturity. In effect both measures are identical; the assumption of uniform reinvestment rate allows us to calculate the IRR as equivalent to the redemption yield. It is common for the IRR measure to be used by corporate financiers for project appraisal, while the redemption yield measure is used in bond markets. The solution to the equation for rm cannot be found analytically and has to be solved through numerical iteration, that is, by estimating the yield from two trial values for rm, then solving by using the formula for linear interpolation. It is more common nowadays to use a spreadsheet programme or programmable calculator such as an Hewlett-Packard calculator.
Using the redemption yield calculation
We have already alluded to the key assumption behind the YTM calculation, namely that the rate rm remains stable for the entire period of the life of the bond. By assuming the same yield we can say that all coupons are reinvested at the same yield rm. This is patently unrealistic since we can predict with virtual certainty that interest rates for instruments of similar maturity to the bond at each coupon date will not remain unchanged. In practice however investors require a rate of return that is equivalent to the price that they are paying for a bond and the redemption yield is, to put it simply, as good a measurement as any. A more accurate measurement might be to calculate present values of future cash flows using the discount rate that is equal to the markets view on where interest rates will be at that point, known as the forward interest rate. However forward rates are implied interest rates, and a YTM measurement calculated using forward rates can be as speculative as one calculated using the conventional formula. This is because the actual market interest rate at any time is invariably different from the rate implied earlier in the forward markets. So a YTM calculation made using forward rates would not be realised in practice either.[1] We shall see later in this chapter how the zero-coupon interest rate is the true interest rate for any term to maturity, however the YTM is, despite the limitations presented by its assumptions, the main measure of return used in the markets.